Research in the Booth group focuses on developing, implementing and applying new computational techniques for the study of many-body physics and chemistry -- specifically trying to understand correlated electron systems. Being able to computationally predict the nature of these systems, their properties and responses to things like light, voltages, temperature and environmental changes, holds huge promise in a wide number of fields, from drug design to developing new materials, and where computers can answer questions about these materials where experiments would have much more difficulty. Do you want to experimentally study the nature of hydrogen at the surface of the sun?! The importance of computational simulation has now grown to such a degree that it is often referred to as a 'third-way' of making scientific discovery, given equal weight to more traditional experimental or theoretical discoveries. Our work involves improving the capabilities of this approach for these correlated electron systems.

What is the problem?

The interactions between electrons and nuclei provide the glue that binds together all materials and chemicals. The specifics of these interactions give rise to the vast array of different properties around us, ranging from metallic behaviour, to catalytic biomolecules or magnetic interactions. However, while it is now common to design large-scale engineering projects from buildings to planes with accurate computational simulation, it is curious that the techniques for microscopic simulations of the interactions of these most fundamental particles is still very much lacking.

As an often used, and particularly impressive example, this picture shows a small cube of ceramic material, which has the amazing ability to levitate above a magnet when sufficiently cooled. It is the coordinated collective motion of the electrons inside the bulk of the material which allow this property to emerge, and despite decades of research, a consensus among scientists about the mechanism behind this emergent behaviour is still lacking. Despite this missing understanding, these materials are still used in MRI scanners, Maglev trains, and many other places. Would an understanding and computational description of these materials and this emergent property enable us to design materials with improved properties, or even understand the mechanisms behind some of the most important biological enzymes that enable life?

The main difficulty in solving these problems comes from the fact that we have many particles (generally electrons), which are all negatively charged, and so repel each other. Therefore, precisely determining the motion of any one particle will depend simultaneously on all other particles. This is what we mean when we say that the motions of all the particles are 'correlated'. The first step is generally to approximate the motion of all other particles by some averaged distribution of the particles you want to move through, but this isn't generally sufficiently accurate. For instance, imagine trying to navigate through a crowd, knowing only what the average position of all the other people in the crowd - you'd end up bumping into a lot of people, and it would certainly not be an optimal route. (This is made even more difficult if the average distribution of the crowd also includes you! This is the so-called self-interaction error in Density Functional Theory). This problem is a very general problem in many situations, known as the 'many-body' problem, and crops up when trying to model the motion of people through crowds, the optimal delivery route of your online shopping delivery van, or indeed the motion of electrons through a material. Unfortunately, the exact solution to these problems requires exponentially increasing computational effort as you increase the number of interacting particles (known as an NP-hard problem), and so to see large-scale behaviour such as the emergence of superconductivity requires far too many particles for even the largest supercomputer to even approach solving.

Modelling quantum particles

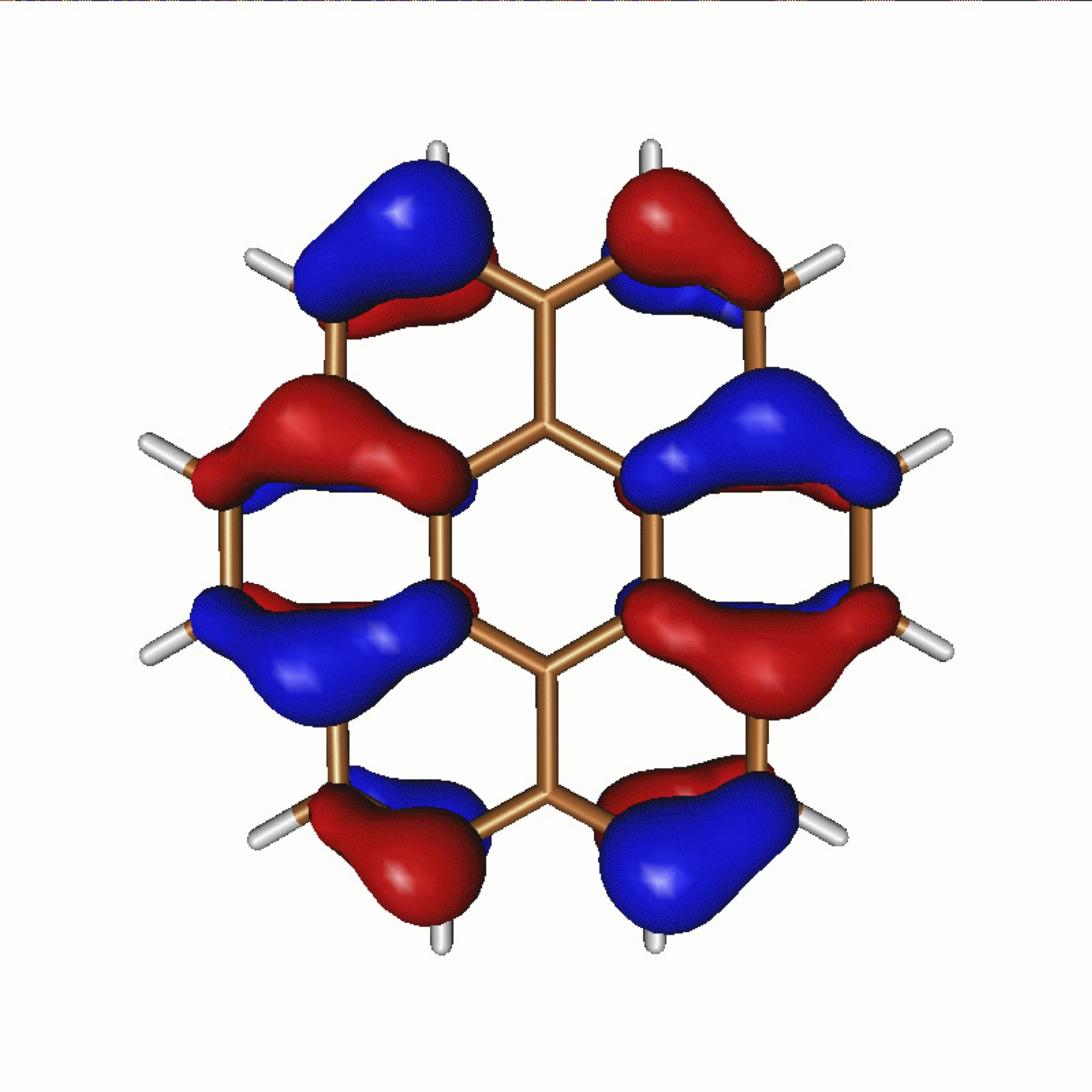While this is a huge problem in itself, when working with electrons we also have to work within the strange world of quantum mechanics. Unlike the examples of the delivery van or person in a crowd, electrons cannot be thought of solely as particles, but also have a wave-like character which has to be considered, giving rise to the electron distributions such as those modelled by us here in an organic coronene molecule. This means that if the path of two electrons is the same, they can not only reinforce each other, but also potentially cancel each other out. Strange effects like swapping the position of two electrons giving rise to a negative distribution of the electrons, which has no analog in traditional distributions, still occupies philosophers and physicists alike in trying to conceptually rationalise this behaviour, but still must be taken into account in our calculations to observe the correct behaviour. The exact solution to the quantum many-body problem therefore does not give at the end a single optimal path for the electrons (as there is for the delivery van), but instead an infinite number of paths, all of which have a positive or negative probability amplitude associated with them. Once we have these, then in principle, all properties of the system can be extracted.

Hopefully, some of the challenges of the field have been described, as well as the importance and potential benefits of being able to make progress in it. Our job is now to develop improved theoretical models, computational algorithms and software to extract these properties of interest without having to rely on experimental input first. This involves understanding the problems, and making considered approximations to ensure that as much of the relevant physical processes from the quantum many-body problem are retained, while making the problem tractable for us. We then write programs and develop software to computationally simulate these systems, ranging from problems in small astrochemical molecules, or biological enzymes, all the way to exotic condensed matter.

For a more technical overview on current research, see our Research page.