Full Configuration Interaction Quantum Monte Carlo

FCIQMC is a recently developed quantum Monte Carlo method (together with Ali Alavi) which shows much promise in the description of correlated systems. It is a stochastic projector Monte Carlo approach which is formulated in the second quantized space of Slater determinants. While this space is exponentially large, the gauge freedom to choose the specific representation allows for a sparse representation of the wavefunction to be found, and annihilation events can then efficiently suppress the manifestation of the 'Fermion sign problem'. Further development is continuing in a number of directions to expand the scope, accuracy and efficiency of the approach in order to apply it to a range of chemical, material and lattice problems. These include:

• Four-component relativistic formulation to treat relativistic and magnetic effects on the same level as electron correlation (with Prof. Toru Shiozaki of Northwestern University, USA)
• Reformulation to compute both static and dynamic response functions from various perturbations
• Multi-scale approaches to combine FCIQMC in a low-energy subspace with high-energy effects, including fully internally-contracted stochastic multireference perturbation theory, and real-space embedding techniques (see below)

Developments in FCIQMC are integrated within our efficient, parallelised NECI code, available to interested researchers for academic use via our github page.

Stochastic Approaches To Tensor Network States

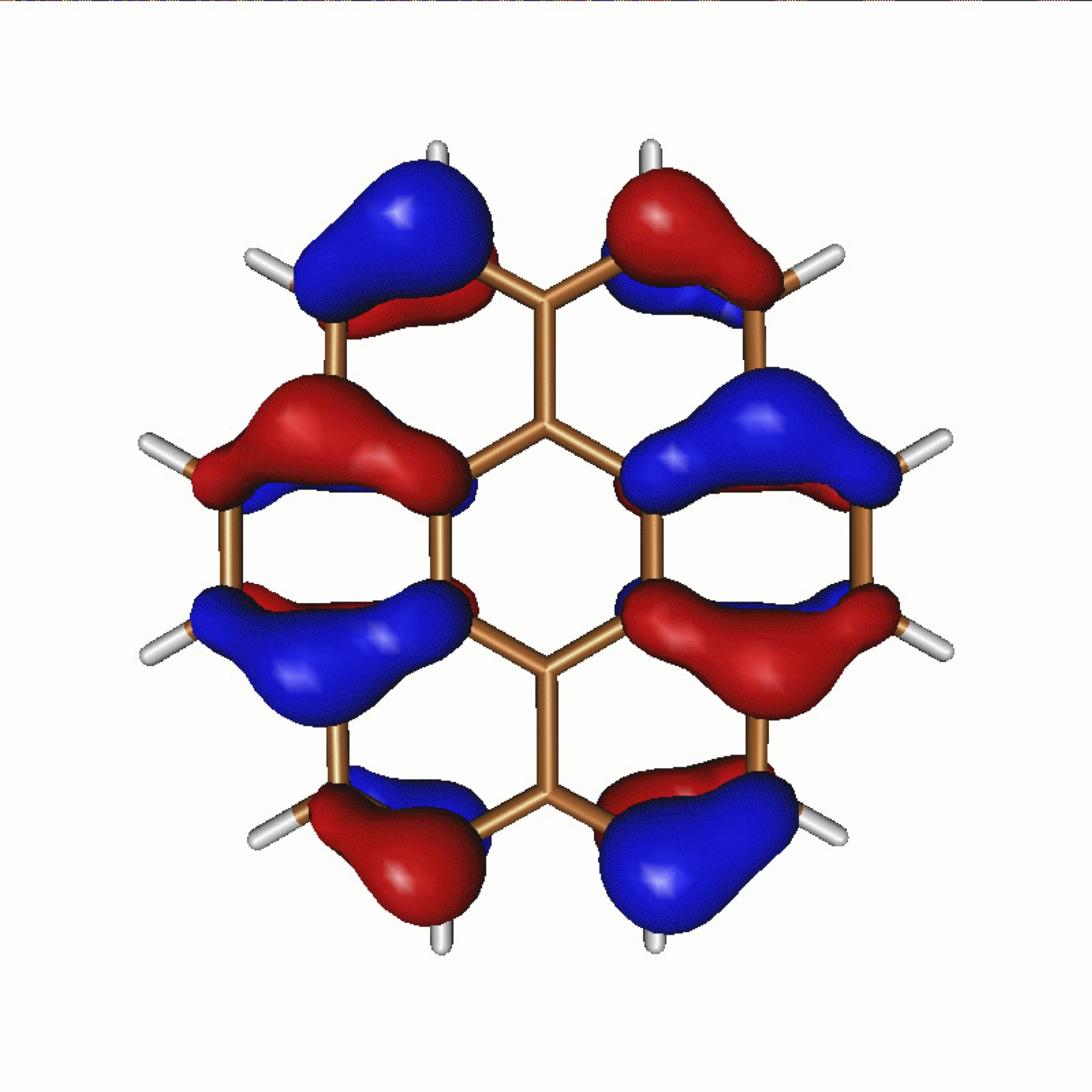
We have been developing new approaches to optimize and stochastically sample certain classes of tensor network states which don't easily admit to an efficient deterministic algorithm. This allows for higher-dimensional networks to be considered, in a scalable approach. The approach combines ideas of projector Monte Carlo with the non-linear form of these Tensor Networks. Additionally, ideas from accelerated optimization techniques used to train neural networks render the approach scalable and robust. The above shows the spin correlation functions derived from this work of a two-dimensional, ab initio graphene sheet, published in Physical Review Letters, 118 176403 (2017). This work has been applied to lattice models, as well as realistic, extended systems, by projecting down to low-energy, reduced subspace models.

Continuing developments are investigating coupling of the optimization to the stochastic sampling of auxiliary indices and moving towards entangled 2D networks, as well as a more efficient coupling to higher-energy degrees of freedom for a truly ab initio method.

Embedded Methods In The Description Of Extended Systems

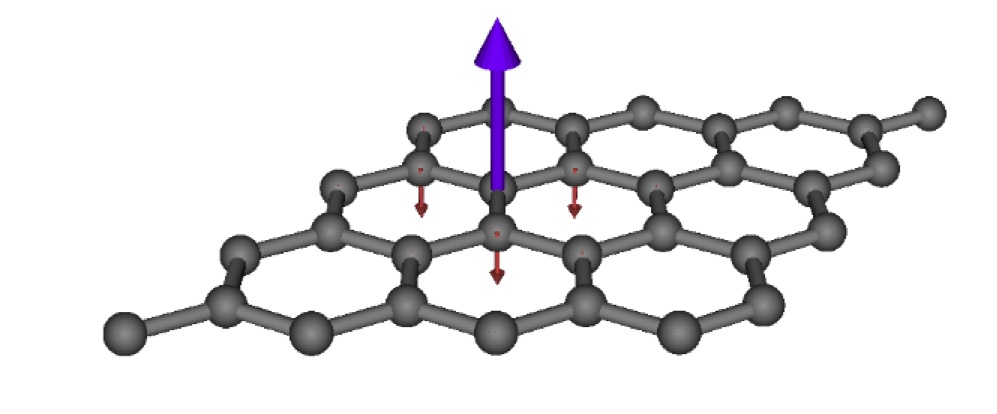
Since two-point correlation functions decay (generally exponentially fast in insulators), we look for ways to exploit this locality to develop quantum embedding approaches. As opposed to more traditional embedding methods such as QM/MM, these approaches allow for quantum fluctuations between the embedded fragment and the environment, and therefore describing the desired mixed quantum state on the fragment. In the condensed matter community, Dynamical Mean-field Theory has been hugely successful in describing the qualitative features of Mott insulating behaviour. However, much of this physics can also be captured in a wavefunction approach known as Density Matrix Embedding Theory (DMET).

Our research in this area concerns a number of aspects to develop these approaches, both for ab initio and lattice models. We are combining the DMET methodology with an LDA bandstructure for realistic materials, and comparing to the successful, but more expensive LDA+DMFT approach in collaboration with Dr. Cedric Weber and the ONETEP code. We are also looking into diagrammatic extensions to the DMET approach, including improved self-consistency conditions based on the self-energy to allow for genuine lattice correlations rather than symmetry-breaking.

Spectral Functions and Theoretical Spectroscopy

Spectral functions define the dynamic response of a system to a perturbation, and are the key quantities in a wide range of theoretical spectroscopy, giving access to the entire excitation spectrum of a system. This makes these quantities often more demanding to compute, and with a poorer range of techniques to reliably compute them compared to static observables. Beyond their utility in spectroscopy, they are often also the key quantum variables in computational methods too -- especially the one-particle greens function.

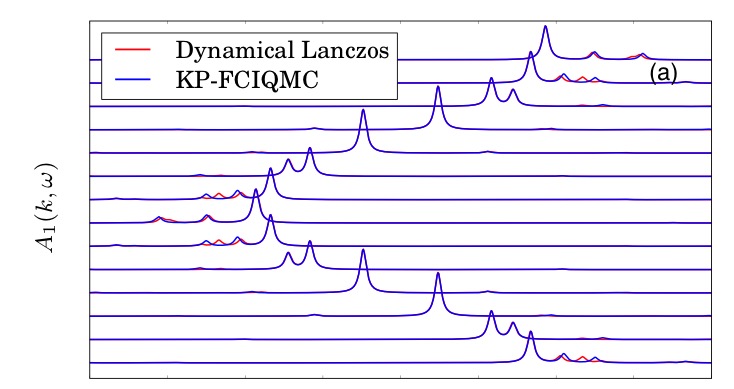
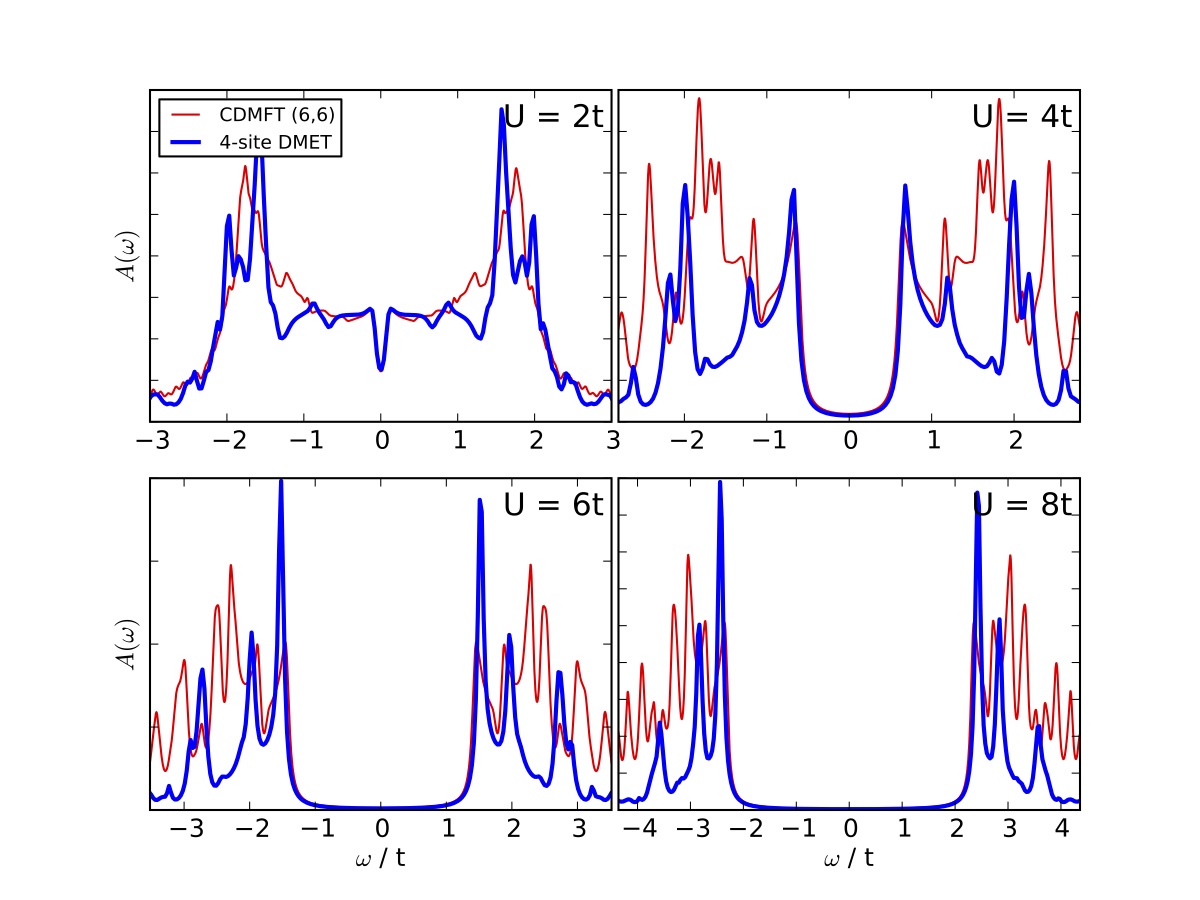
We are developing new approaches to compute correlated spectral functions of systems, including stochastic techniques, and cavity approximations from statistical physics. In addition, these spectra are used to develop new approaches to multireference quantum chemistry, circumventing the need for high-rank density matrices to couple the active space to the dynamic correlation, and providing a fully screened description of the effective interactions. Above shows the bandstructure of the Hubbard model computed via a stochastic Krylov projection technique, described in Physical Review Letters, 115, 050603 (2015).

Machine Learning of Quantum Systems

Can we infer a fully correlated wavefunction, with only partial knowledge of the amplitudes at particular points? The domain of machine learning has expanded in recent years into a powerful approach for inference and interpolation of complex functions. In collaboration with Prof. Gábor Csányi, we are investigating approaches of using Gaussian Processes to describe an extensive and complete wavefunction which can capture strong correlation effects.

Time Evolution of Electronic States

New generations of time-resolved spectroscopy and cold-atom experiments are pushing the capabilities of computational approaches to study wave packets out of equilibrium, and in response to sudden changes in potentials. Stochastic dynamics are being devised based on time-dependent variational principles to access longer time scales of correlated phenomena beyond the linear response regime.

This work is being undertaken in collaboration with Dr. Joe Bhaseen as part of the CANES CDT in non-equilibrium systems.

Software Infrastructure

We see an important part of developing new computational methods as ensuring that they are accessible to the wider community, to enable as wide a cross-section of researchers as possible to use these tools for their own purposes. This means that the group has a strong expertise in programming and developing accessible and efficient software. Furthermore, in order for these methods to compete with established methods and implementations, the developed codes need to be fast, robust, and parallelise across many computing cores. The need for this efficiency and scalability affects every design decision we make, from the nature of the approximations and development of the theory, to the implementation in terms of optimized algorithms.

To this end, we have a number of software packages which we develop in for different purposes. We are core developers of the NECI software package, developed for efficient, parallelised FCIQMC calculations for a number of different systems. However, we also develop in a number of other packages, including PySCF, MOLPRO, VASP and others, depending on which code is best suited to the task at hand.

Applications

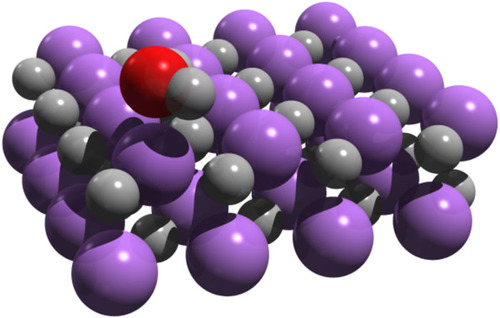
All methodological development in the group is motivated by applications of interest which are not adequately treated within established approximations and techniques. These span a wide array of quantum many-body problems, from strongly-correlated lattice models, such as the Hubbard or Heisenberg lattices, the high-accuracy description of small astrochemical molecules, the understanding of mechanisms of biological active sites, or the ab initio treatment of crystalline materials.

Above is one such example, showing the absorption of water onto a Lithium Hydride surface - something which is poorly treated due to the lack of accurate dispersion interactions in Density Functional Theory, described in the paper entitled "A comparison between quantum chemistry and quantum Monte Carlo techniques for the adsorption of water on the (001) LiH surface".